Computes power/Type I error and expected sample size for a group sequential
design across a selected set of parameter values for a given set of analyses
and boundaries. The print function has been extended using
print.gsProbability to print gsProbability objects; see
examples.
Depending on the calling sequence, an object of class gsProbability
or class gsDesign is returned. If it is of class gsDesign then
the members of the object will be the same as described in
gsDesign. If d is input as NULL (the default),
all other arguments (other than r) must be specified and an object of
class gsProbability is returned. If d is passed as an object
of class gsProbability or gsDesign the only other argument
required is theta; the object returned has the same class as the
input d. On output, the values of theta input to
gsProbability will be the parameter values for which the design is
characterized.
Usage
gsProbability(k = 0, theta, n.I, a, b, r = 18, d = NULL, overrun = 0)
# S3 method for class 'gsProbability'
print(x, ...)Arguments
- k
Number of analyses planned, including interim and final.
- theta
Vector of standardized effect sizes for which boundary crossing probabilities are to be computed.
- n.I
Sample size or relative sample size at analyses; vector of length k. See
gsDesignand manual.- a
Lower bound cutoffs (z-values) for futility or harm at each analysis, vector of length k.
- b
Upper bound cutoffs (z-values) for futility at each analysis; vector of length k.
- r
Integer value (>= 1 and <= 80) controlling the number of numerical integration grid points. Default is 18, as recommended by Jennison and Turnbull (2000). Grid points are spread out in the tails for accurate probability calculations. Larger values provide more grid points and greater accuracy but slow down computation. Jennison and Turnbull (p. 350) note an accuracy of \(10^{-6}\) with
r = 16. This parameter is normally not changed by users.- d
If not
NULL, this should be an object of typegsDesignreturned by a call togsDesign(). When this is specified, the values ofk,n.I,a,b, andrwill be obtained fromdand onlythetaneeds to be specified by the user.- overrun
Scalar or vector of length
k-1with patients enrolled that are not included in each interim analysis.- x
An item of class
gsProbability.- ...
Not implemented (here for compatibility with generic print input).
Value
- k
As input.
- theta
As input.
- n.I
As input.
- lower
A list containing two elements:
boundis as input inaandprobis a matrix of boundary crossing probabilities. Elementi,jcontains the boundary crossing probability at analysisifor thej-th element ofthetainput. All boundary crossing is assumed to be binding for this computation; that is, the trial must stop if a boundary is crossed.- upper
A list of the same form as
lowercontaining the upper bound and upper boundary crossing probabilities.- en
A vector of the same length as
thetacontaining expected sample sizes for the trial design corresponding to each value in the vectortheta.- r
As input.
Note:
print.gsProbability() returns the input x.
Note
The gsDesign technical manual is available at https://keaven.github.io/gsd-tech-manual/.
References
Jennison C and Turnbull BW (2000), Group Sequential Methods with Applications to Clinical Trials. Boca Raton: Chapman and Hall.
Author
Keaven Anderson keaven_anderson@merck.com
Examples
library(ggplot2)
# making a gsDesign object first may be easiest...
x <- gsDesign()
# take a look at it
x
#> Asymmetric two-sided group sequential design with
#> 90 % power and 2.5 % Type I Error.
#> Upper bound spending computations assume
#> trial continues if lower bound is crossed.
#>
#> Sample
#> Size ----Lower bounds---- ----Upper bounds-----
#> Analysis Ratio* Z Nominal p Spend+ Z Nominal p Spend++
#> 1 0.357 -0.24 0.4057 0.0148 3.01 0.0013 0.0013
#> 2 0.713 0.94 0.8267 0.0289 2.55 0.0054 0.0049
#> 3 1.070 2.00 0.9772 0.0563 2.00 0.0228 0.0188
#> Total 0.1000 0.0250
#> + lower bound beta spending (under H1):
#> Hwang-Shih-DeCani spending function with gamma = -2.
#> ++ alpha spending:
#> Hwang-Shih-DeCani spending function with gamma = -4.
#> * Sample size ratio compared to fixed design with no interim
#>
#> Boundary crossing probabilities and expected sample size
#> assume any cross stops the trial
#>
#> Upper boundary (power or Type I Error)
#> Analysis
#> Theta 1 2 3 Total E{N}
#> 0.0000 0.0013 0.0049 0.0171 0.0233 0.6249
#> 3.2415 0.1412 0.4403 0.3185 0.9000 0.7913
#>
#> Lower boundary (futility or Type II Error)
#> Analysis
#> Theta 1 2 3 Total
#> 0.0000 0.4057 0.4290 0.1420 0.9767
#> 3.2415 0.0148 0.0289 0.0563 0.1000
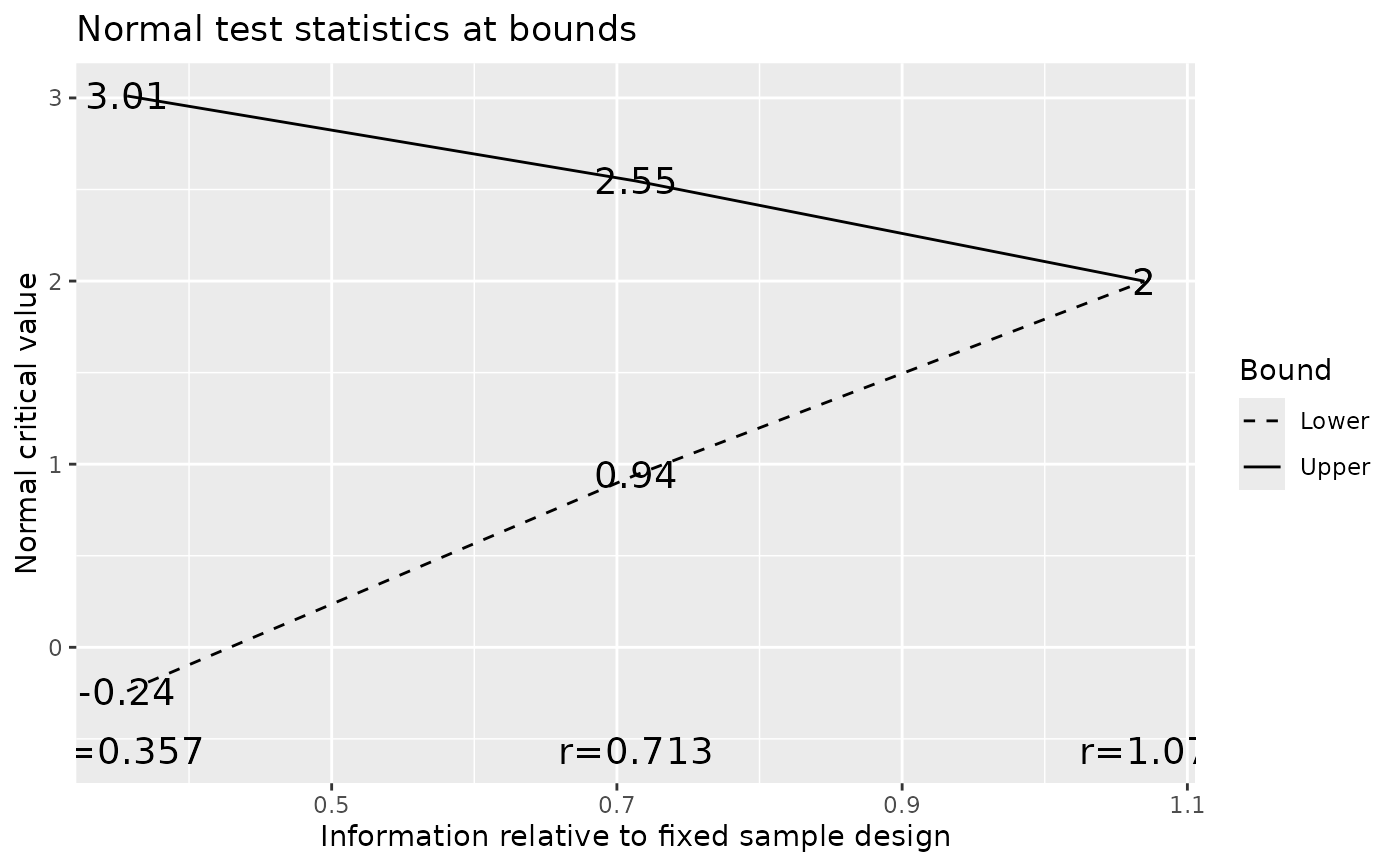
# default plot for gsDesign object shows boundaries
plot(x)
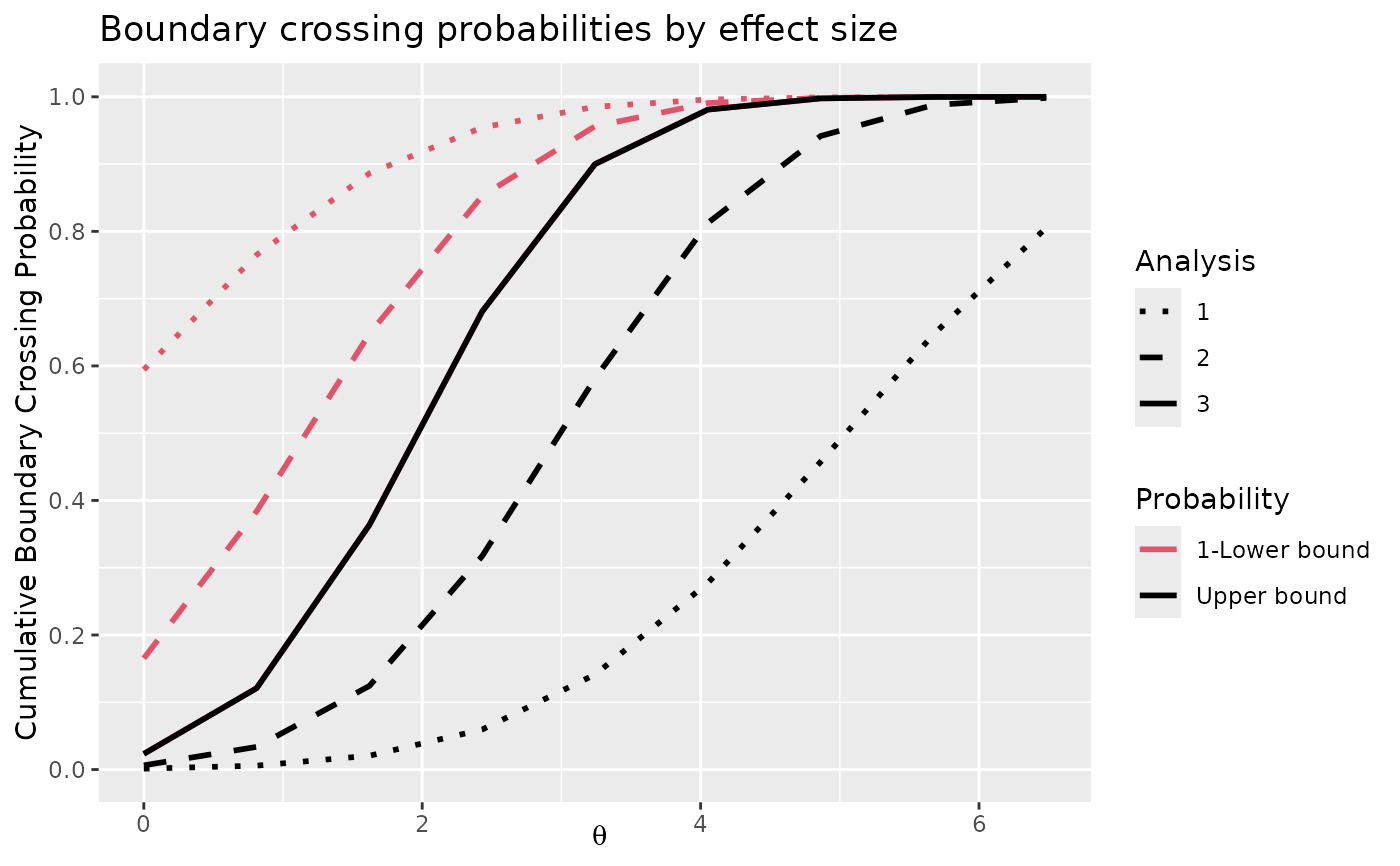
 # \code{plottype=2} shows boundary crossing probabilities
plot(x, plottype = 2)
# \code{plottype=2} shows boundary crossing probabilities
plot(x, plottype = 2)
 # now add boundary crossing probabilities and
# expected sample size for more theta values
y <- gsProbability(d = x, theta = x$delta * seq(0, 2, .25))
class(y)
#> [1] "gsDesign"
# note that "y" below is equivalent to \code{print(y)} and
# \code{print.gsProbability(y)}
y
#> Asymmetric two-sided group sequential design with
#> 90 % power and 2.5 % Type I Error.
#> Upper bound spending computations assume
#> trial continues if lower bound is crossed.
#>
#> Sample
#> Size ----Lower bounds---- ----Upper bounds-----
#> Analysis Ratio* Z Nominal p Spend+ Z Nominal p Spend++
#> 1 0.357 -0.24 0.4057 0.0148 3.01 0.0013 0.0013
#> 2 0.713 0.94 0.8267 0.0289 2.55 0.0054 0.0049
#> 3 1.070 2.00 0.9772 0.0563 2.00 0.0228 0.0188
#> Total 0.1000 0.0250
#> + lower bound beta spending (under H1):
#> Hwang-Shih-DeCani spending function with gamma = -2.
#> ++ alpha spending:
#> Hwang-Shih-DeCani spending function with gamma = -4.
#> * Sample size ratio compared to fixed design with no interim
#>
#> Boundary crossing probabilities and expected sample size
#> assume any cross stops the trial
#>
#> Upper boundary (power or Type I Error)
#> Analysis
#> Theta 1 2 3 Total E{N}
#> 0.0000 0.0013 0.0049 0.0171 0.0233 0.6249
#> 0.8104 0.0058 0.0279 0.0872 0.1209 0.7523
#> 1.6208 0.0205 0.1038 0.2393 0.3636 0.8520
#> 2.4311 0.0595 0.2579 0.3636 0.6810 0.8668
#> 3.2415 0.1412 0.4403 0.3185 0.9000 0.7913
#> 4.0519 0.2773 0.5353 0.1684 0.9810 0.6765
#> 4.8623 0.4574 0.4844 0.0559 0.9976 0.5701
#> 5.6727 0.6469 0.3410 0.0119 0.9998 0.4868
#> 6.4830 0.8053 0.1930 0.0016 1.0000 0.4266
#>
#> Lower boundary (futility or Type II Error)
#> Analysis
#> Theta 1 2 3 Total
#> 0.0000 0.4057 0.4290 0.1420 0.9767
#> 0.8104 0.2349 0.3812 0.2630 0.8791
#> 1.6208 0.1138 0.2385 0.2841 0.6364
#> 2.4311 0.0455 0.1017 0.1718 0.3190
#> 3.2415 0.0148 0.0289 0.0563 0.1000
#> 4.0519 0.0039 0.0054 0.0097 0.0190
#> 4.8623 0.0008 0.0006 0.0009 0.0024
#> 5.6727 0.0001 0.0001 0.0000 0.0002
#> 6.4830 0.0000 0.0000 0.0000 0.0000
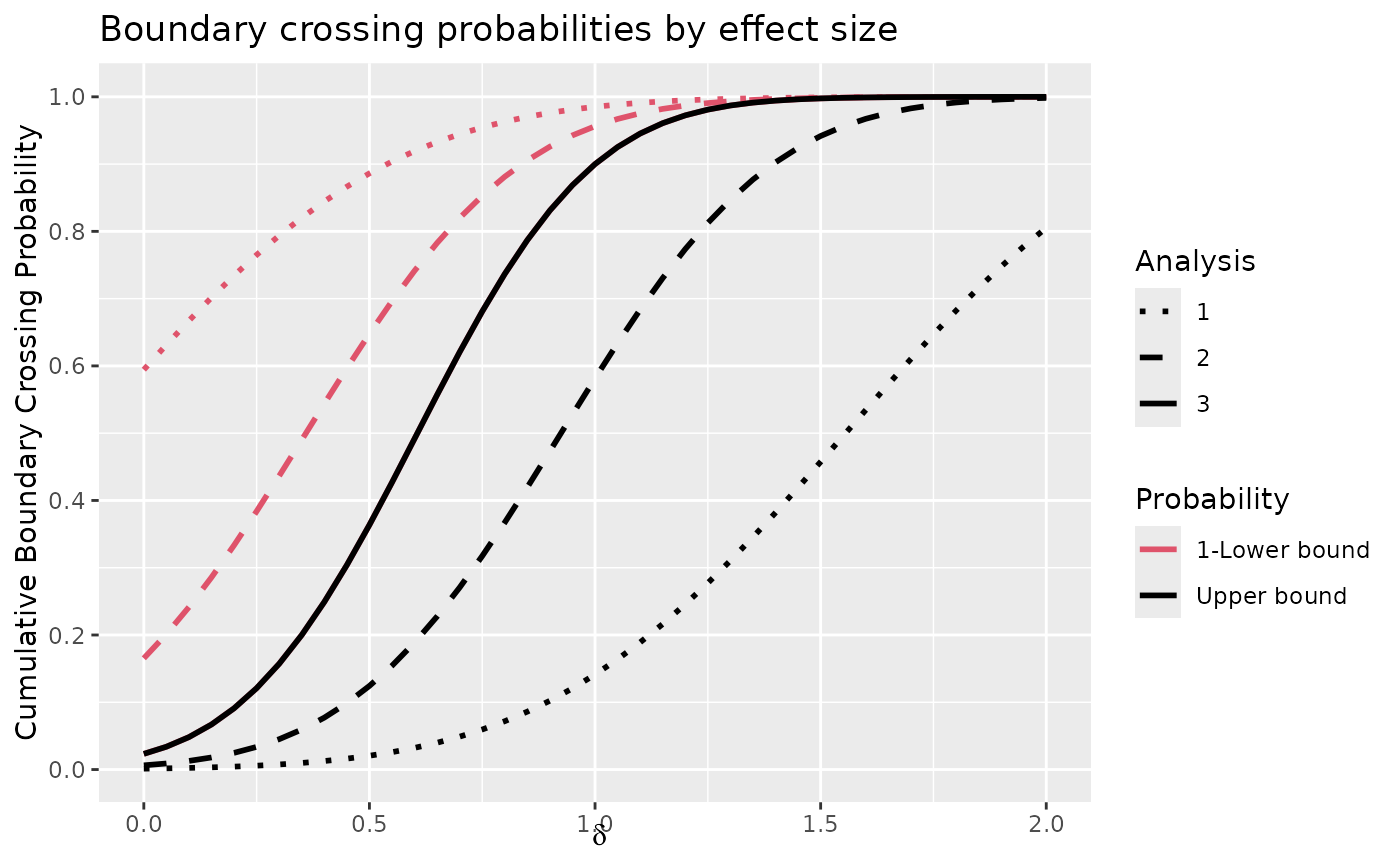
# the plot does not change from before since this is a
# gsDesign object; note that theta/delta is on x axis
plot(y, plottype = 2)
# now add boundary crossing probabilities and
# expected sample size for more theta values
y <- gsProbability(d = x, theta = x$delta * seq(0, 2, .25))
class(y)
#> [1] "gsDesign"
# note that "y" below is equivalent to \code{print(y)} and
# \code{print.gsProbability(y)}
y
#> Asymmetric two-sided group sequential design with
#> 90 % power and 2.5 % Type I Error.
#> Upper bound spending computations assume
#> trial continues if lower bound is crossed.
#>
#> Sample
#> Size ----Lower bounds---- ----Upper bounds-----
#> Analysis Ratio* Z Nominal p Spend+ Z Nominal p Spend++
#> 1 0.357 -0.24 0.4057 0.0148 3.01 0.0013 0.0013
#> 2 0.713 0.94 0.8267 0.0289 2.55 0.0054 0.0049
#> 3 1.070 2.00 0.9772 0.0563 2.00 0.0228 0.0188
#> Total 0.1000 0.0250
#> + lower bound beta spending (under H1):
#> Hwang-Shih-DeCani spending function with gamma = -2.
#> ++ alpha spending:
#> Hwang-Shih-DeCani spending function with gamma = -4.
#> * Sample size ratio compared to fixed design with no interim
#>
#> Boundary crossing probabilities and expected sample size
#> assume any cross stops the trial
#>
#> Upper boundary (power or Type I Error)
#> Analysis
#> Theta 1 2 3 Total E{N}
#> 0.0000 0.0013 0.0049 0.0171 0.0233 0.6249
#> 0.8104 0.0058 0.0279 0.0872 0.1209 0.7523
#> 1.6208 0.0205 0.1038 0.2393 0.3636 0.8520
#> 2.4311 0.0595 0.2579 0.3636 0.6810 0.8668
#> 3.2415 0.1412 0.4403 0.3185 0.9000 0.7913
#> 4.0519 0.2773 0.5353 0.1684 0.9810 0.6765
#> 4.8623 0.4574 0.4844 0.0559 0.9976 0.5701
#> 5.6727 0.6469 0.3410 0.0119 0.9998 0.4868
#> 6.4830 0.8053 0.1930 0.0016 1.0000 0.4266
#>
#> Lower boundary (futility or Type II Error)
#> Analysis
#> Theta 1 2 3 Total
#> 0.0000 0.4057 0.4290 0.1420 0.9767
#> 0.8104 0.2349 0.3812 0.2630 0.8791
#> 1.6208 0.1138 0.2385 0.2841 0.6364
#> 2.4311 0.0455 0.1017 0.1718 0.3190
#> 3.2415 0.0148 0.0289 0.0563 0.1000
#> 4.0519 0.0039 0.0054 0.0097 0.0190
#> 4.8623 0.0008 0.0006 0.0009 0.0024
#> 5.6727 0.0001 0.0001 0.0000 0.0002
#> 6.4830 0.0000 0.0000 0.0000 0.0000
# the plot does not change from before since this is a
# gsDesign object; note that theta/delta is on x axis
plot(y, plottype = 2)
 # now let's see what happens with a gsProbability object
z <- gsProbability(
k = 3, a = x$lower$bound, b = x$upper$bound,
n.I = x$n.I, theta = x$delta * seq(0, 2, .25)
)
# with the above form, the results is a gsProbability object
class(z)
#> [1] "gsProbability"
z
#> Lower bounds Upper bounds
#> Analysis N Z Nominal p Z Nominal p
#> 1 1 -0.24 0.4057 3.01 0.0013
#> 2 1 0.94 0.8267 2.55 0.0054
#> 3 2 2.00 0.9772 2.00 0.0228
#>
#> Boundary crossing probabilities and expected sample size assume
#> any cross stops the trial
#>
#> Upper boundary
#> Analysis
#> Theta 1 2 3 Total E{N}
#> 0.0000 0.0013 0.0049 0.0171 0.0233 0.6
#> 0.8104 0.0058 0.0279 0.0872 0.1209 0.8
#> 1.6208 0.0205 0.1038 0.2393 0.3636 0.9
#> 2.4311 0.0595 0.2579 0.3636 0.6810 0.9
#> 3.2415 0.1412 0.4403 0.3185 0.9000 0.8
#> 4.0519 0.2773 0.5353 0.1684 0.9810 0.7
#> 4.8623 0.4574 0.4844 0.0559 0.9976 0.6
#> 5.6727 0.6469 0.3410 0.0119 0.9998 0.5
#> 6.4830 0.8053 0.1930 0.0016 1.0000 0.4
#>
#> Lower boundary
#> Analysis
#> Theta 1 2 3 Total
#> 0.0000 0.4057 0.4290 0.1420 0.9767
#> 0.8104 0.2349 0.3812 0.2630 0.8791
#> 1.6208 0.1138 0.2385 0.2841 0.6364
#> 2.4311 0.0455 0.1017 0.1718 0.3190
#> 3.2415 0.0148 0.0289 0.0563 0.1000
#> 4.0519 0.0039 0.0054 0.0097 0.0190
#> 4.8623 0.0008 0.0006 0.0009 0.0024
#> 5.6727 0.0001 0.0001 0.0000 0.0002
#> 6.4830 0.0000 0.0000 0.0000 0.0000
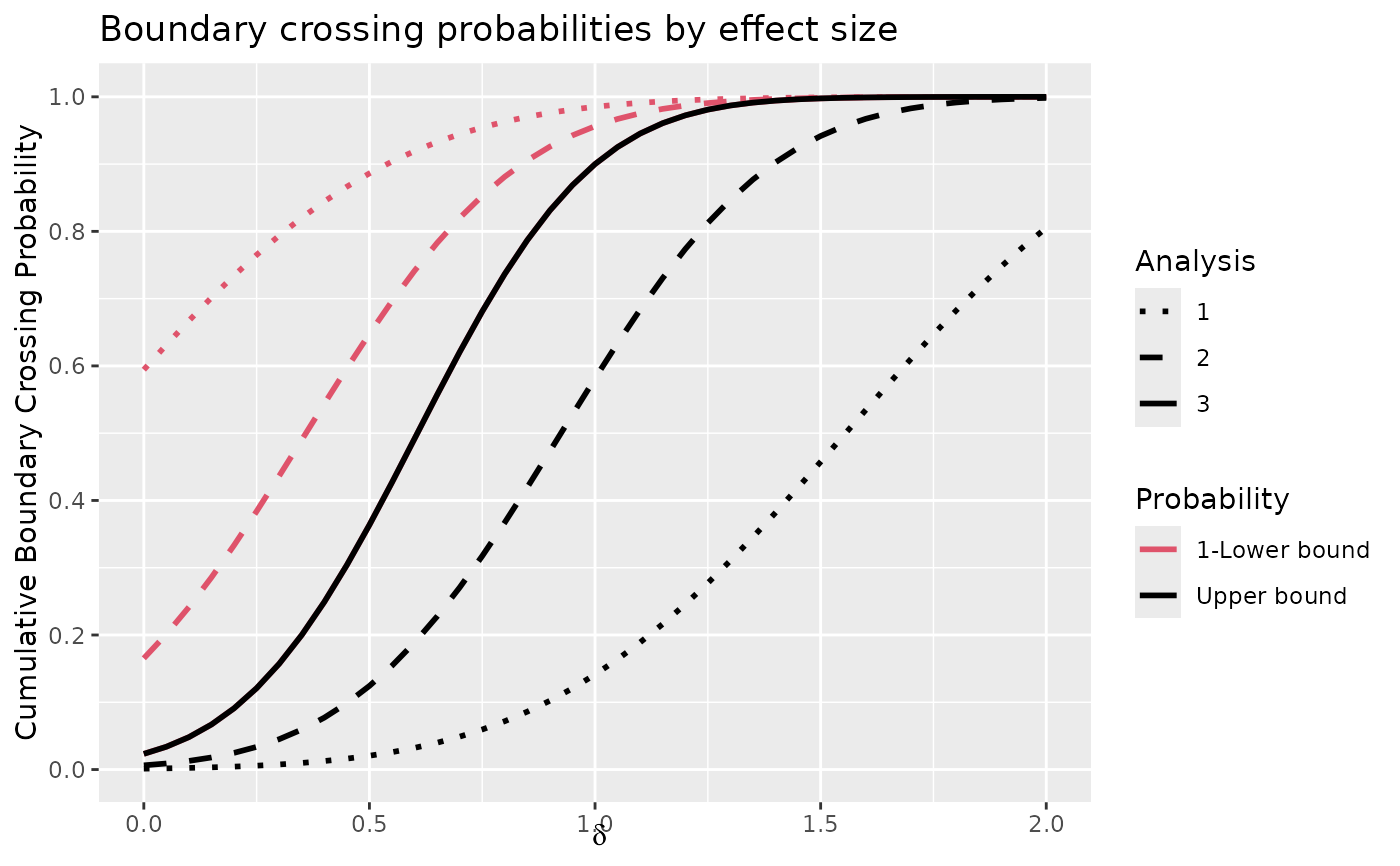
# default plottype is now 2
# this is the same range for theta, but plot now has theta on x axis
plot(z)
# now let's see what happens with a gsProbability object
z <- gsProbability(
k = 3, a = x$lower$bound, b = x$upper$bound,
n.I = x$n.I, theta = x$delta * seq(0, 2, .25)
)
# with the above form, the results is a gsProbability object
class(z)
#> [1] "gsProbability"
z
#> Lower bounds Upper bounds
#> Analysis N Z Nominal p Z Nominal p
#> 1 1 -0.24 0.4057 3.01 0.0013
#> 2 1 0.94 0.8267 2.55 0.0054
#> 3 2 2.00 0.9772 2.00 0.0228
#>
#> Boundary crossing probabilities and expected sample size assume
#> any cross stops the trial
#>
#> Upper boundary
#> Analysis
#> Theta 1 2 3 Total E{N}
#> 0.0000 0.0013 0.0049 0.0171 0.0233 0.6
#> 0.8104 0.0058 0.0279 0.0872 0.1209 0.8
#> 1.6208 0.0205 0.1038 0.2393 0.3636 0.9
#> 2.4311 0.0595 0.2579 0.3636 0.6810 0.9
#> 3.2415 0.1412 0.4403 0.3185 0.9000 0.8
#> 4.0519 0.2773 0.5353 0.1684 0.9810 0.7
#> 4.8623 0.4574 0.4844 0.0559 0.9976 0.6
#> 5.6727 0.6469 0.3410 0.0119 0.9998 0.5
#> 6.4830 0.8053 0.1930 0.0016 1.0000 0.4
#>
#> Lower boundary
#> Analysis
#> Theta 1 2 3 Total
#> 0.0000 0.4057 0.4290 0.1420 0.9767
#> 0.8104 0.2349 0.3812 0.2630 0.8791
#> 1.6208 0.1138 0.2385 0.2841 0.6364
#> 2.4311 0.0455 0.1017 0.1718 0.3190
#> 3.2415 0.0148 0.0289 0.0563 0.1000
#> 4.0519 0.0039 0.0054 0.0097 0.0190
#> 4.8623 0.0008 0.0006 0.0009 0.0024
#> 5.6727 0.0001 0.0001 0.0000 0.0002
#> 6.4830 0.0000 0.0000 0.0000 0.0000
# default plottype is now 2
# this is the same range for theta, but plot now has theta on x axis
plot(z)