Diagnosing Blinded Information Calculation Issues • gsDesignNB

Overview

This vignette examines two problematic datasets where the blinded information calculation produced extreme values. Understanding these edge cases helps inform potential improvements to the calculate_blinded_info() function.

We examine two scenarios:

Near-zero blinded information: Cases where blinded_info is essentially 0 despite reasonable unblinded_info
Extreme high blinded information: Cases where blinded_info is astronomically large (10^38)

Both scenarios arise from instability in the negative binomial model fitting on blinded (pooled) data.

library(gsDesignNB)
library(data.table)
library(ggplot2)
library(MASS)

Dataset 1: Near-Zero Blinded Information

This dataset was identified from simulations where blinded_info = 0.02 while unblinded_info = 48.6 — a ratio of 0.0004.

# Load the problematic dataset
# Try package location first, fall back to relative path for development
data_path <- system.file("extdata", "problematic_dataset.rds", package = "gsDesignNB")
if (data_path == "") {
  # During development, find the package root
  data_path <- file.path("..", "inst", "extdata", "problematic_dataset.rds")
}
cut_data <- readRDS(data_path)
dt <- as.data.table(cut_data)

Event Counts Summary

# Overall summary
cat("Total subjects:", nrow(dt), "\n")
#> Total subjects: 360
cat("Total events:", sum(dt$events), "\n")
#> Total events: 209
cat("Mean events per subject:", round(mean(dt$events), 3), "\n")
#> Mean events per subject: 0.581
cat("Variance of events:", round(var(dt$events), 3), "\n")
#> Variance of events: 0.79
cat("Variance/Mean ratio:", round(var(dt$events) / mean(dt$events), 3), "\n")
#> Variance/Mean ratio: 1.361

# By treatment
dt[, .(
  n = .N,
  total_events = sum(events),
  mean_events = round(mean(events), 3),
  var_events = round(var(events), 3),
  pct_zero_events = round(100 * mean(events == 0), 1)
), by = treatment]
#>       treatment     n total_events mean_events var_events pct_zero_events
#>          <char> <int>        <int>       <num>      <num>           <num>
#> 1:      control   180          132       0.733      0.979            55.6
#> 2: experimental   180           77       0.428      0.559            68.3

Event Distribution

# Event count distribution
event_dist <- dt[, .(count = .N), by = .(treatment, events)]
event_dist[order(treatment, events)]
#>        treatment events count
#>           <char>  <int> <int>
#>  1:      control      0   100
#>  2:      control      1    45
#>  3:      control      2    19
#>  4:      control      3    15
#>  5:      control      4     1
#>  6: experimental      0   123
#>  7: experimental      1    44
#>  8: experimental      2     7
#>  9: experimental      3     5
#> 10: experimental      4     1

A key observation is the high proportion of subjects with zero events, particularly in the experimental arm.

Event Rates by Patient

We calculate the event rate as events divided by follow-up duration (tte).

dt[, event_rate := events / tte]

# Summary of event rates
dt[, .(
  n = .N,
  mean_rate = round(mean(event_rate), 4),
  median_rate = round(median(event_rate), 4),
  sd_rate = round(sd(event_rate), 4),
  pct_zero_rate = round(100 * mean(event_rate == 0), 1)
), by = treatment]
#>       treatment     n mean_rate median_rate sd_rate pct_zero_rate
#>          <char> <int>     <num>       <num>   <num>         <num>
#> 1:      control   180    0.1624           0  0.2847          55.6
#> 2: experimental   180    1.2725           0 15.8474          68.3

Violin Plot of Event Rates

# Add overall group for comparison
dt_plot <- rbind(
  dt[, .(treatment = treatment, event_rate = event_rate)],
  dt[, .(treatment = "Overall (Pooled)", event_rate = event_rate)]
)

ggplot(dt_plot, aes(x = treatment, y = event_rate, fill = treatment)) +
  geom_violin(alpha = 0.7, scale = "width") +
  geom_boxplot(width = 0.1, fill = "white", alpha = 0.8) +
  labs(
    title = "Distribution of Patient-Level Event Rates",
    subtitle = "Dataset with Near-Zero Blinded Information",
    x = "Treatment Group",
    y = "Event Rate (events / follow-up time)"
  ) +
  theme_minimal() +
  theme(legend.position = "none") +
  scale_fill_brewer(palette = "Set2")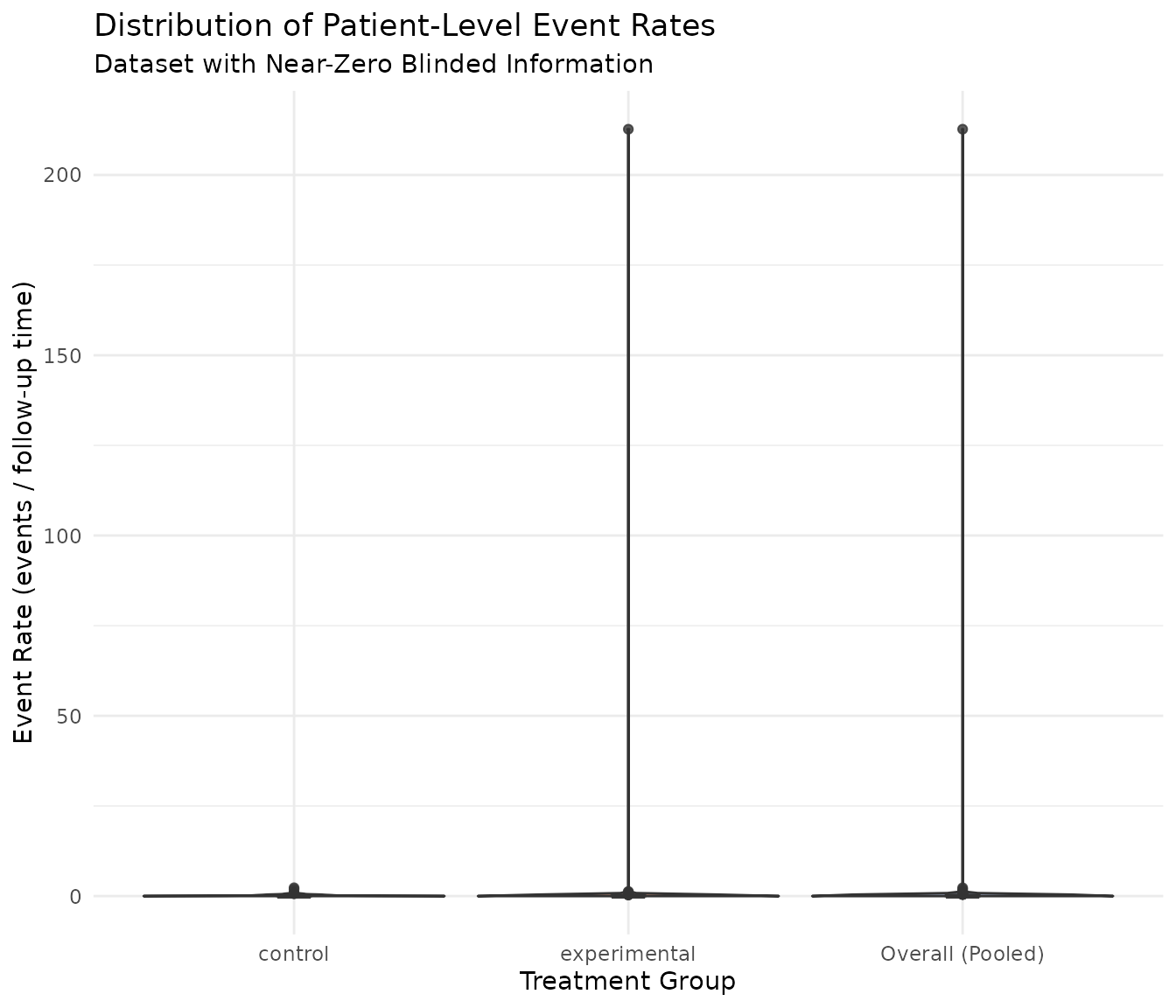

The violin plot shows that many subjects have zero event rates, creating a spike at zero. The control arm has higher event rates than the experimental arm, as expected given the simulation parameters.

What Happened with the Information Calculations

# Blinded information calculation
blinded_res <- calculate_blinded_info(
  cut_data,
  ratio = 1,
  lambda1_planning = 1.5/12,
  lambda2_planning = 1.0/12
)

cat("Blinded Information Results:\n")
#> Blinded Information Results:
cat("  blinded_info:", blinded_res$blinded_info, "\n")
#>   blinded_info: 0.0201878
cat("  dispersion_blinded:", blinded_res$dispersion_blinded, "\n")
#>   dispersion_blinded: 4454.477
cat("  lambda_blinded:", blinded_res$lambda_blinded, "\n")
#>   lambda_blinded: 0.6791599

# Unblinded calculation via mutze_test
mutze_res <- mutze_test(cut_data)

cat("\nUnblinded (Mutze Test) Results:\n")
#> 
#> Unblinded (Mutze Test) Results:
cat("  method:", mutze_res$method, "\n")
#>   method: Poisson Wald (fallback)
cat("  SE:", round(mutze_res$se, 4), "\n")
#>   SE: 0.1434
cat("  unblinded_info (1/SE^2):", round(1/mutze_res$se^2, 2), "\n")
#>   unblinded_info (1/SE^2): 48.63
cat("  dispersion:", mutze_res$dispersion, "\n")
#>   dispersion: Inf

Root Cause Analysis

The issue stems from the blinded glm.nb fit:

df <- as.data.frame(cut_data)
df <- df[df$tte > 0, ]

# Blinded fit (no treatment effect)
fit_blinded <- suppressWarnings(MASS::glm.nb(events ~ 1 + offset(log(tte)), data = df))

cat("Blinded glm.nb fit:\n")
#> Blinded glm.nb fit:
cat("  theta:", fit_blinded$theta, "\n")
#>   theta: 0.0002244933
cat("  1/theta (dispersion):", 1/fit_blinded$theta, "\n")
#>   1/theta (dispersion): 4454.477

# Unblinded fit (with treatment effect)
fit_unblinded <- suppressWarnings(MASS::glm.nb(events ~ treatment + offset(log(tte)), data = df))

cat("\nUnblinded glm.nb fit:\n")
#> 
#> Unblinded glm.nb fit:
cat("  theta:", fit_unblinded$theta, "\n")
#>   theta: 0.000138869
cat("  1/theta (dispersion):", 1/fit_unblinded$theta, "\n")
#>   1/theta (dispersion): 7201.033

The Problem: The blinded glm.nb fit returns an extremely small theta (≈ 0.0002), which translates to dispersion_blinded = 1/theta ≈ 4454.

The blinded information formula is: \[w_j = p_j \sum_i \frac{\mu_{ij}}{1 + k \cdot \mu_{ij}}\]

where \(k\) is the dispersion and \(\mu_{ij} = \lambda_j \cdot t_i\).

When \(k\) is very large (4454), the denominator becomes huge: \[1 + 4454 \times 0.5 \approx 2228\]

This makes \(w_j\) approximately 2000 times smaller than it should be, causing the information to collapse to near-zero.

Method of Moments Comparison

Here we compare the problematic MLE estimate with the Method of Moments (MoM) estimator.

# Calculate MoM estimates
mom_res <- estimate_nb_mom(df)

cat("Method of Moments (Blinded) Estimation:\n")
#> Method of Moments (Blinded) Estimation:
cat("  Lambda (Rate):", round(mom_res$lambda, 4), "\n")
#>   Lambda (Rate): 0.1169
cat("  Dispersion (k):", round(mom_res$dispersion, 4), "\n")
#>   Dispersion (k): 0.3292

The MoM estimator produces a much more reasonable dispersion estimate compared to the MLE’s 4454. This suggests the MoM approach is more robust to this specific data distribution where the “blinded” assumption (single rate) is violated by the treatment effect.

Dataset 2: Extreme High Blinded Information

This dataset was identified from simulation 630 in the group-sequential simulation, where blinded_info = 1.84 × 10^38 — an astronomically large value indicating numerical overflow.

# Load the extreme high dataset (reproduced from simulation 630)
data_path_2 <- system.file("extdata", "extreme_high_dataset.rds", package = "gsDesignNB")
if (data_path_2 == "") {
  data_path_2 <- file.path("..", "inst", "extdata", "extreme_high_dataset.rds")
}
cut_data_2 <- readRDS(data_path_2)
dt2 <- as.data.table(cut_data_2)

Event Counts Summary

# Overall summary
cat("Total subjects:", nrow(dt2), "\n")
#> Total subjects: 313
cat("Total events:", sum(dt2$events), "\n")
#> Total events: 116
cat("Mean events per subject:", round(mean(dt2$events), 3), "\n")
#> Mean events per subject: 0.371
cat("Variance of events:", round(var(dt2$events), 3), "\n")
#> Variance of events: 0.458
cat("Variance/Mean ratio:", round(var(dt2$events) / mean(dt2$events), 3), "\n")
#> Variance/Mean ratio: 1.237

# By treatment
dt2[, .(
  n = .N,
  total_events = sum(events),
  mean_events = round(mean(events), 3),
  var_events = round(var(events), 3),
  pct_zero_events = round(100 * mean(events == 0), 1)
), by = treatment]
#>       treatment     n total_events mean_events var_events pct_zero_events
#>          <char> <int>        <int>       <num>      <num>           <num>
#> 1: Experimental   156           42       0.269      0.314            78.2
#> 2:      Control   157           74       0.471      0.584            66.2

What Happened with the Information Calculations

# Blinded information calculation
blinded_res_2 <- calculate_blinded_info(
  cut_data_2,
  ratio = 1,
  lambda1_planning = 1.5/12,
  lambda2_planning = 1.0/12
)

cat("Blinded Information Results:\n")
#> Blinded Information Results:
cat("  blinded_info:", format(blinded_res_2$blinded_info, scientific = TRUE), "\n")
#>   blinded_info: 1.826963e+38
cat("  dispersion_blinded:", format(blinded_res_2$dispersion_blinded, scientific = TRUE), "\n")
#>   dispersion_blinded: 5.875129e-42
cat("  lambda_blinded:", round(blinded_res_2$lambda_blinded, 4), "\n")
#>   lambda_blinded: 6.078207e+35

# Unblinded calculation via mutze_test
mutze_res_2 <- mutze_test(cut_data_2)

cat("\nUnblinded (Mutze Test) Results:\n")
#> 
#> Unblinded (Mutze Test) Results:
cat("  method:", mutze_res_2$method, "\n")
#>   method: Poisson Wald (fallback)
cat("  SE:", round(mutze_res_2$se, 4), "\n")
#>   SE: 0.1932
cat("  unblinded_info (1/SE^2):", round(1/mutze_res_2$se^2, 2), "\n")
#>   unblinded_info (1/SE^2): 26.79
cat("  dispersion:", mutze_res_2$dispersion, "\n")
#>   dispersion: Inf

Root Cause Analysis

df2 <- as.data.frame(cut_data_2)
df2 <- df2[df2$tte > 0, ]

# Blinded fit (no treatment effect)
fit_blinded_2 <- tryCatch(
  suppressWarnings(MASS::glm.nb(events ~ 1 + offset(log(tte)), data = df2)),
  error = function(e) NULL
)

if (!is.null(fit_blinded_2)) {
  cat("Blinded glm.nb fit:\n")
  cat("  theta:", format(fit_blinded_2$theta, scientific = TRUE), "\n")
  cat("  1/theta (dispersion):", format(1/fit_blinded_2$theta, scientific = TRUE), "\n")
} else {
  cat("Blinded glm.nb fit FAILED\n")
}
#> Blinded glm.nb fit:
#>   theta: 1.70209e+41 
#>   1/theta (dispersion): 5.875129e-42

# Unblinded fit (with treatment effect)
fit_unblinded_2 <- tryCatch(
  suppressWarnings(MASS::glm.nb(events ~ treatment + offset(log(tte)), data = df2)),
  error = function(e) NULL
)

if (!is.null(fit_unblinded_2)) {
  cat("\nUnblinded glm.nb fit:\n")
  cat("  theta:", round(fit_unblinded_2$theta, 4), "\n")
  cat("  1/theta (dispersion):", round(1/fit_unblinded_2$theta, 4), "\n")
} else {
  cat("\nUnblinded glm.nb fit FAILED - this explains the Poisson fallback\n")
}
#> 
#> Unblinded glm.nb fit FAILED - this explains the Poisson fallback

The Problem: The blinded glm.nb returns an astronomically large theta (≈ 1.7 × 10^41), which translates to dispersion_blinded ≈ 5.9 × 10^-42 — essentially zero.

The information formula depends on: \[w_j = p_j \sum_i \frac{\mu_{ij}}{1 + k \cdot \mu_{ij}}\]

When \(k \to 0\): \[w_j \approx p_j \sum_i \mu_{ij}\]

This makes \(w_j\) very large, and since variance = \(1/w_1 + 1/w_2\), the variance approaches zero, causing information = 1/variance to overflow to infinity.

Method of Moments Comparison

Again, we compare with the Method of Moments (MoM) estimator.

# Calculate MoM estimates
mom_res_2 <- estimate_nb_mom(df2)

cat("Method of Moments (Blinded) Estimation:\n")
#> Method of Moments (Blinded) Estimation:
cat("  Lambda (Rate):", round(mom_res_2$lambda, 4), "\n")
#>   Lambda (Rate): 0.0926
cat("  Dispersion (k):", mom_res_2$dispersion, "\n")
#>   Dispersion (k): 0.403252

In this case, the MoM estimator likely returns a positive dispersion (or 0 if underdispersed), avoiding the numerical instability of the infinite theta from the MLE.

Why the Mutze Test Falls Back to Poisson

Note that mutze_test reports dispersion = Inf and uses the “Poisson Wald (fallback)” method. This happens because glm.nb with the treatment effect also struggles with this dataset — the theta estimate becomes unstable, and the function falls back to a simpler Poisson model.

Summary of Issues

Issue	Blinded Info	Cause	Dispersion (blinded)
Near-zero	0.02	Extremely large dispersion estimate	4454
Near-infinite	1.84×10^38	Extremely small dispersion estimate	~0

Both issues arise from instability in glm.nb when fitting to pooled (blinded) data. The pooling can create artificial variance patterns that don’t represent the true data-generating process.

Recommendations

Bound the dispersion estimate: Cap dispersion_blinded to a reasonable range (e.g., 0.01 to 100)
Use assumed dispersion: Consider using the planned/assumed dispersion from the design rather than estimating from blinded data
Add sanity checks: Flag cases where blinded info differs from unblinded info by more than a factor of 2-3
Fallback to unblinded: When blinded estimation produces extreme values, fall back to the unblinded information
Use Method of Moments (MoM): The analysis above demonstrates that a simple Method of Moments estimator is far more robust than glm.nb for blinded parameter estimation in these edge cases. It provides reasonable dispersion estimates even when the blinded MLE fails or returns boundary values.

sessionInfo()
#> R version 4.5.2 (2025-10-31)
#> Platform: x86_64-pc-linux-gnu
#> Running under: Ubuntu 24.04.3 LTS
#> 
#> Matrix products: default
#> BLAS:   /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 
#> LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so;  LAPACK version 3.12.0
#> 
#> locale:
#>  [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8       
#>  [4] LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8    LC_MESSAGES=C.UTF-8   
#>  [7] LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C          
#> [10] LC_TELEPHONE=C         LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C   
#> 
#> time zone: UTC
#> tzcode source: system (glibc)
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#> [1] MASS_7.3-65         ggplot2_4.0.2       data.table_1.18.2.1
#> [4] gsDesignNB_0.2.6   
#> 
#> loaded via a namespace (and not attached):
#>  [1] gt_1.3.0            sass_0.4.10         future_1.69.0      
#>  [4] generics_0.1.4      tidyr_1.3.2         xml2_1.5.2         
#>  [7] r2rtf_1.3.0         lattice_0.22-7      listenv_0.10.0     
#> [10] digest_0.6.39       magrittr_2.0.4      evaluate_1.0.5     
#> [13] grid_4.5.2          RColorBrewer_1.1-3  iterators_1.0.14   
#> [16] mvtnorm_1.3-3       fastmap_1.2.0       Matrix_1.7-4       
#> [19] foreach_1.5.2       simtrial_1.0.2      jsonlite_2.0.0     
#> [22] survival_3.8-3      purrr_1.2.1         scales_1.4.0       
#> [25] codetools_0.2-20    textshaping_1.0.4   jquerylib_0.1.4    
#> [28] cli_3.6.5           rlang_1.1.7         parallelly_1.46.1  
#> [31] future.apply_1.20.1 splines_4.5.2       withr_3.0.2        
#> [34] cachem_1.1.0        yaml_2.3.12         gsDesign_3.8.0     
#> [37] tools_4.5.2         parallel_4.5.2      doFuture_1.2.0     
#> [40] dplyr_1.2.0         globals_0.19.0      vctrs_0.7.1        
#> [43] R6_2.6.1            lifecycle_1.0.5     fs_1.6.6           
#> [46] htmlwidgets_1.6.4   ragg_1.5.0          pkgconfig_2.0.3    
#> [49] desc_1.4.3          pkgdown_2.2.0       pillar_1.11.1      
#> [52] bslib_0.10.0        gtable_0.3.6        glue_1.8.0         
#> [55] Rcpp_1.1.1          systemfonts_1.3.1   xfun_0.56          
#> [58] tibble_3.3.1        tidyselect_1.2.1    knitr_1.51         
#> [61] farver_2.1.2        xtable_1.8-4        htmltools_0.5.9    
#> [64] labeling_0.4.3      rmarkdown_2.30      compiler_4.5.2     
#> [67] S7_0.2.1