Sample size calculation for negative binomial outcomes
Source:vignettes/sample-size-nbinom.Rmd
sample-size-nbinom.RmdThis vignette describes the methodology used in the
sample_size_nbinom function for calculating sample sizes
when comparing two treatment groups with negative binomial outcomes.
Methodology
We wish to test for differences in rates of recurrent events between two treatment groups using a negative binomial model to account for overdispersion. The underlying test is to evaluate the log rate ratio between the two groups. This is parameterized in terms of event rates \(\lambda_1\) and \(\lambda_2\) (events per unit time) for the control and treatment groups, respectively. The usual null hypothesis is that the rates are equal (\(H_0: \lambda_1 = \lambda_2\)) with a one-sided alternative (\(H_1: \lambda_1 > \lambda_2\)). However, non-inferiority or equivalence tests can also be performed by specifying an appropriate null hypothesis.
Negative binomial distribution
We assume the outcome \(Y\) follows a negative binomial distribution with mean \(\mu\) and a common dispersion parameter \(k\) for both treatment groups, such that the variance is given by:
\[ \mathrm{Var}(Y) = \mu + k \mu^2 \]
Note that in R’s rnbinom parameterization, \(k = 1/\texttt{size}\).
Connection between rates and counts
The negative binomial distribution can be motivated by a Gamma-Poisson mixture model. Suppose that for each subject \(i\), the event rate \(\Lambda_i\) is a random variable following a Gamma distribution with shape \(\alpha = 1/k\) and rate \(\beta = 1/(k \lambda)\), where \(\lambda\) is the underlying population event rate and \(k\) is the dispersion parameter. The mean of this Gamma distribution is \(\mathrm{E}[\Lambda_i] = \alpha / \beta = \lambda\) and the variance is \(\mathrm{Var}(\Lambda_i) = \alpha / \beta^2 = k \lambda^2\).
Given the subject-specific rate \(\Lambda_i\), the number of events \(Y_i\) observed over a time period \(t_i\) follows a Poisson distribution with rate \(\Lambda_i t_i\): \[ Y_i | \Lambda_i \sim \text{Poisson}(\Lambda_i t_i) \]
The marginal distribution of \(Y_i\) (integrating out \(\Lambda_i\)) is then a negative binomial distribution with mean \(\mu_i = \lambda t_i\) and dispersion parameter \(k\). The variance is: \[ \mathrm{Var}(Y_i) = \mathrm{E}[\mathrm{Var}(Y_i|\Lambda_i)] + \mathrm{Var}(\mathrm{E}[Y_i|\Lambda_i]) \] \[ = \mathrm{E}[\Lambda_i t_i] + \mathrm{Var}(\Lambda_i t_i) \] \[ = \lambda t_i + t_i^2 (k \lambda^2) \] \[ = \mu_i + k \mu_i^2 \]
This formulation connects the event rate \(\lambda\) (used in the hypothesis testing framework) with the expected count \(\mu\) (used in the negative binomial parameterization), showing how heterogeneity in individual rates leads to the overdispersion characteristic of the negative binomial distribution.
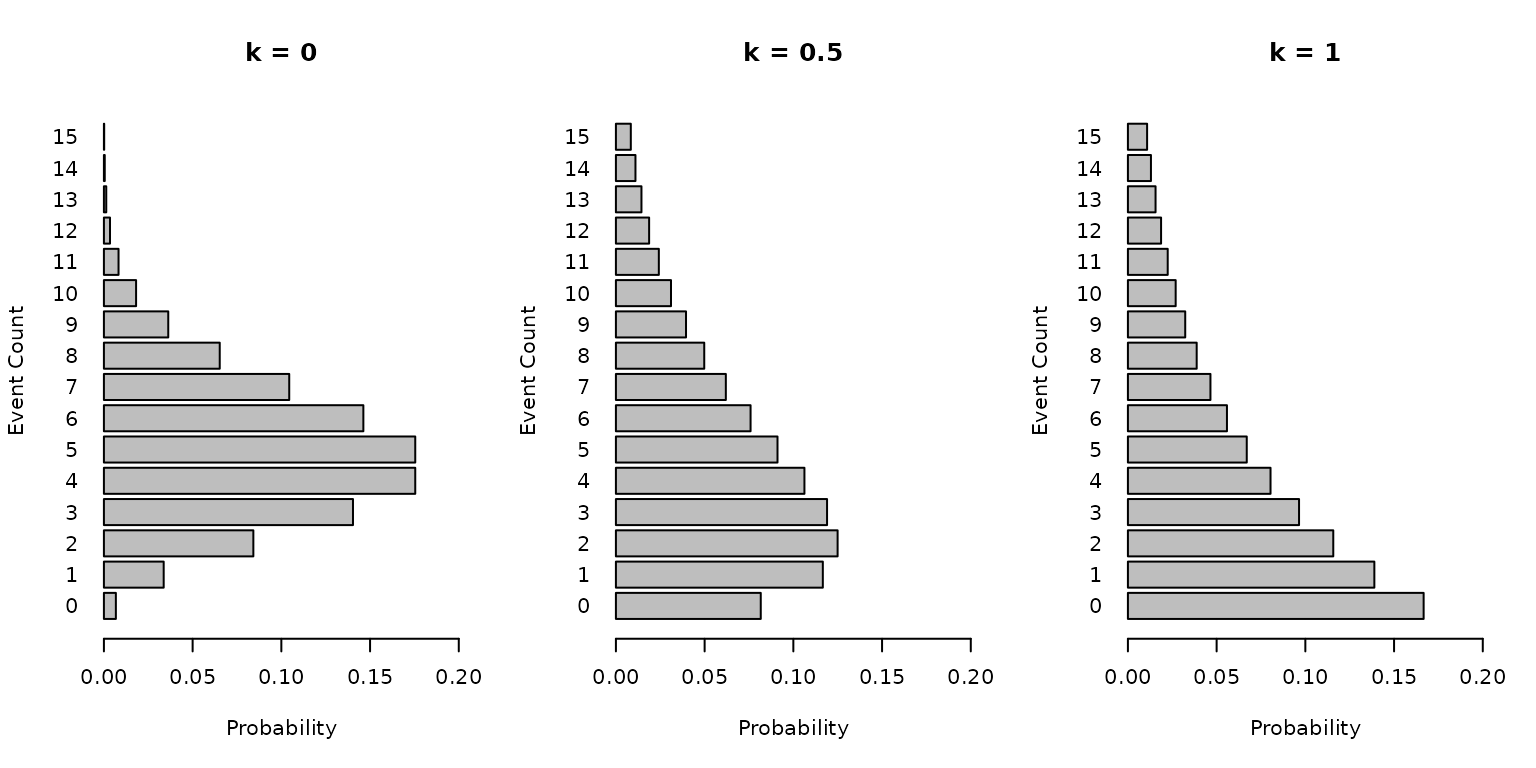
Graphical representation of negative binomial distributions
In the following panel, we illustrate an expected value of 5 events over a fixed time period for different dispersion parameters \(k\) (0, 0.5, 1). As \(k\) increases, the variance increases, leading to a wider spread of possible event counts.
par(mfrow = c(1, 3))
k_values <- c(0, 0.5, 1)
for (k in k_values) {
mu <- 5
x <- 0:15
if (k == 0) {
probs <- dpois(x, lambda = mu)
} else {
size <- 1 / k
probs <- dnbinom(x, size = size, mu = mu)
}
barplot(probs,
names.arg = x, horiz = TRUE, main = paste("k =", k),
xlab = "Probability", ylab = "Event Count", las = 1, xlim = c(0, 0.2)
)
}
Sample size formula
The sample size calculation is based on the asymptotic normality of
the log rate ratio, \(\theta = \log(\lambda_2
/ \lambda_1)\). This approach corresponds to Method
3 of Zhu and Lakkis (2014), which
uses a Wald statistic for the log rate ratio. It is also the method
described by Friede and Schmidli (2010)
and Mütze et al. (2019) (as implemented in
the gscounts package).
The total sample size \(n_{\text{total}}\) is calculated as:
\[ n_{\text{total}} = \frac{(z_{\alpha/s} + z_{\beta})^2 \cdot \tilde{V}}{(\theta - \theta_0)^2} \]
where:
- \(z_{\alpha/s}\) and \(z_{\beta}\) are the standard normal critical values for the significance level \(\alpha\) (with \(s=1\) or \(2\) sided) and power \(1-\beta\).
- \(\theta = \log(\lambda_2 / \lambda_1)\) is the log rate ratio.
- \(\theta_0\) is the log rate ratio under the null hypothesis (default is 0 for superiority).
- \(\tilde{V}\) is the average variance per subject for \(\hat{\theta} = \log(\widehat{\lambda_2 / \lambda_1})\), defined as:
\[ \tilde{V} = \frac{1/ \mu_1 + k}{p_1} + \frac{1/ \mu_2 + k}{p_2} \]
where:
- \(p_1 = n_1/n_{\text{total}}\) and \(p_2 = n_2/n_{\text{total}}\) are the allocation proportions.
- \(\mu_i = \lambda_i \cdot \bar{t}\) is the expected mean count for group \(i\) over the average exposure duration \(\bar{t}\).
-
\(k\) is the dispersion parameter.
While the cited literature assumes a common dispersion parameter across
groups,
sample_size_nbinom()allows for different dispersion parameters \(k_1\) and \(k_2\) for the control and treatment groups, respectively. In this case, the variance formula becomes:
\[ \tilde{V} = \frac{1/ \mu_1 + k_1}{p_1} + \frac{1/ \mu_2 + k_2}{p_2} \]
This formula assumes that the exposure duration is the same for both
groups (or uses an average exposure \(\bar{t}\)). However,
sample_size_nbinom() allows for different dropout rates for
the two groups, which results in different average exposure durations
\(\bar{t}_1\) and \(\bar{t}_2\). In this case, \(\mu_1 = \lambda_1 \bar{t}_1\) and \(\mu_2 = \lambda_2 \bar{t}_2\). Also, when
the assumed gap between events is > 0, the expected exposure is
impacted differently for each group based on their event rates.
Non-inferiority and Super-superiority
The parameter rr0 (\(\theta_0\)) allows for testing
non-inferiority or super-superiority hypotheses. The null hypothesis is
\(H_0: \lambda_2 / \lambda_1 \ge
\theta_0\) (assuming lower rates are better).
- Superiority (default): \(\theta_0 = 1\). We test if the treatment rate is lower than the control rate.
- Non-inferiority: \(\theta_0 > 1\) (e.g., 1.1). We test if the treatment rate is not worse than the control rate by more than a margin of 10%.
- Super-superiority: \(\theta_0 < 1\) (e.g., 0.8). We test if the treatment rate is better than the control rate by at least 20%.
Average exposure with variable accrual and dropout
When the accrual rate is not constant or when the trial has a fixed
duration with ongoing recruitment, the exposure time for patients will
vary. The function calculates an average exposure time to use
in the sample size formula. Additionally, if a dropout_rate
is specified, the exposure is adjusted to account for patients leaving
the study early.
Let \(T\) be the total trial duration. Suppose recruitment occurs in \(J\) segments, where the \(j\)-th segment has accrual rate \(R_j\) and duration \(D_j\).
If dropout_rate is 0:
- The expected number of patients recruited in segment \(j\) is \(N_j = R_j \cdot D_j\).
- The start time of segment \(j\) is \(S_{j-1} = \sum_{i=1}^{j-1} D_i\) (with \(S_0 = 0\)).
- The midpoint of recruitment for segment \(j\) is \(M_j = S_{j-1} + D_j/2\).
- The average follow-up (exposure) time for patients recruited in segment \(j\) is approximately \(E_j = T - M_j\).
If dropout_rate (\(\delta\)) > 0, the average exposure is
calculated by integrating the exposure function over the recruitment
interval:
\[ \begin{aligned} E_j &= \frac{1}{D_j}\int_{u_\text{min}}^{u_\text{max}} \frac{1 - e^{-\delta u}}{\delta} du \\ &= \frac{1}{\delta} - \frac{1}{\delta^2 D_j} \left( e^{-\delta u_\text{min}} - e^{-\delta u_\text{max}} \right) \end{aligned} \] where \(u_\text{max}\) and \(u_\text{min}\) are the maximum and minimum potential follow-up times for patients in that segment (\(T - S_{j-1}\) and \(T - (S_{j-1} + D_j)\) respectively).
Group-specific parameters
The function supports specifying dropout_rate as a
vector of length 2, corresponding to the control and treatment groups
respectively. This allows for scenarios where the dropout rate differs
between arms.
If these parameters differ, the average exposure is calculated separately for each group (\(\bar{t}_1\) and \(\bar{t}_2\)). The variance inflation factor \(Q\) (see below) is also calculated separately for each group (\(Q_1\) and \(Q_2\)).
Maximum follow-up
If max_followup (\(F\))
is specified, the follow-up time for any individual is capped at \(F\). This creates three scenarios for a
recruitment segment:
- All truncated: If \(u_\text{min} \ge F\), all patients in the segment have potential follow-up \(\ge F\), so their actual follow-up is \(F\) (subject to dropout).
- None truncated: If \(u_\text{max} \le F\), no patients reach the cap \(F\) before the trial ends. The calculation is as above.
- Partial truncation: If \(u_\text{min} < F < u_\text{max}\), patients recruited earlier in the segment are capped at \(F\), while those recruited later are followed until the trial end. The segment is split into two parts for calculation.
The overall average exposure used for the calculation is the weighted average:
\[ \bar{t} = \frac{\sum_{j=1}^J N_j E_j}{\sum_{j=1}^J N_j} \]
Variance inflation for variable follow-up
When follow-up times are variable (due to accrual, dropout, or administrative censoring), simply using the average follow-up time \(\bar{t}\) in the variance formula underestimates the true variance of the rate estimator. This is because the variance of the negative binomial distribution depends on the exposure time in a non-linear way (\(\mathrm{Var}(Y) = \mu + k\mu^2 = \lambda t + k (\lambda t)^2\)).
To account for this, we apply a variance inflation factor \(Q\) to the dispersion parameter \(k\), as derived by Zhu and Lakkis (2014):
\[ Q = \frac{\mathrm{E}[t^2]}{(\mathrm{E}[t])^2} \]
The adjusted dispersion parameter used in the sample size calculation is \(k_{\text{adj}} = k \cdot Q\). The function automatically calculates \(\mathrm{E}[t]\) and \(\mathrm{E}[t^2]\) based on the accrual, dropout, and trial duration parameters. If exposure differs between groups, \(Q\) is calculated separately for each group.
Event gaps
In some clinical trials, there is a mandatory “dead time” or gap
after an event during which no new events can occur (e.g., a recovery
period). If an event_gap is specified, the effective
exposure time for a subject is reduced by the time spent in these
gaps.
The function approximates the effective event rate as: \[ \lambda_{\text{eff}} \approx \frac{\lambda}{1 + \lambda \cdot \text{gap}} \] This adjusted rate is then used in the sample size calculations. The effective exposure time reported is also adjusted similarly.
Examples
Basic calculation (Zhu and Lakkis 2014)
Calculate sample size for:
- Control rate \(\lambda_1 = 0.5\)
- Treatment rate \(\lambda_2 = 0.3\)
- Dispersion \(k = 0.1\)
- Power = 80%
- Alpha = 0.025 (one-sided)
- Accrual over 12 months
- Trial duration 12 months (implying exposure average of 6 months)
sample_size_nbinom(
lambda1 = 0.5,
lambda2 = 0.3,
dispersion = 0.1,
power = 0.8,
alpha = 0.025,
sided = 1,
accrual_rate = 10, # arbitrary, just for average exposure
accrual_duration = 12,
trial_duration = 12
)
#> Sample size for negative binomial outcome
#> ==========================================
#>
#> Sample size: n1 = 35, n2 = 35, total = 70
#> Expected events: 168.0 (n1: 105.0, n2: 63.0)
#> Power: 80%, Alpha: 0.025 (1-sided)
#> Rates: control = 0.5000, treatment = 0.3000 (RR = 0.6000)
#> Dispersion: 0.1000, Avg exposure (calendar): 6.00
#> Accrual: 12.0, Trial duration: 12.0Piecewise constant accrual
Consider a trial where recruitment ramps up:
- 5 patients/month for the first 3 months
- 10 patients/month for the next 3 months
- Total trial duration is 12 months
The function automatically calculates the average exposure based on this accrual pattern.
sample_size_nbinom(
lambda1 = 0.5,
lambda2 = 0.3,
dispersion = 0.1,
power = 0.8,
accrual_rate = c(5, 10),
accrual_duration = c(3, 3),
trial_duration = 12
)
#> Sample size for negative binomial outcome
#> ==========================================
#>
#> Sample size: n1 = 26, n2 = 26, total = 52
#> Expected events: 176.8 (n1: 110.5, n2: 66.3)
#> Power: 80%, Alpha: 0.025 (1-sided)
#> Rates: control = 0.5000, treatment = 0.3000 (RR = 0.6000)
#> Dispersion: 0.1000, Avg exposure (calendar): 8.50
#> Accrual: 6.0, Trial duration: 12.0Accrual with dropout and max follow-up
Same design as above, but with a 5% dropout rate per unit time and a maximum follow-up of 6 months.
sample_size_nbinom(
lambda1 = 0.5,
lambda2 = 0.3,
dispersion = 0.1,
power = 0.8,
accrual_rate = c(5, 10),
accrual_duration = c(3, 3),
trial_duration = 12,
dropout_rate = 0.05,
max_followup = 6
)
#> Sample size for negative binomial outcome
#> ==========================================
#>
#> Sample size: n1 = 38, n2 = 38, total = 76
#> Expected events: 157.6 (n1: 98.5, n2: 59.1)
#> Power: 80%, Alpha: 0.025 (1-sided)
#> Rates: control = 0.5000, treatment = 0.3000 (RR = 0.6000)
#> Dispersion: 0.1000, Avg exposure (calendar): 5.18
#> Dropout rate: 0.0500
#> Accrual: 6.0, Trial duration: 12.0
#> Max follow-up: 6.0Group-specific dropout rates
Suppose the control group has a higher dropout rate (10%) than the treatment group (5%).
sample_size_nbinom(
lambda1 = 0.5,
lambda2 = 0.3,
dispersion = 0.1,
power = 0.8,
accrual_rate = c(5, 10),
accrual_duration = c(3, 3),
trial_duration = 12,
dropout_rate = c(0.10, 0.05), # Control, Treatment
max_followup = 6
)
#> Sample size for negative binomial outcome
#> ==========================================
#>
#> Sample size: n1 = 40, n2 = 40, total = 80
#> Expected events: 152.4 (n1: 90.2, n2: 62.2)
#> Power: 80%, Alpha: 0.025 (1-sided)
#> Rates: control = 0.5000, treatment = 0.3000 (RR = 0.6000)
#> Dispersion: 0.1000, Avg exposure (calendar): 4.51 (n1), 5.18 (n2)
#> Dropout rate: 0.1000 (n1), 0.0500 (n2)
#> Accrual: 6.0, Trial duration: 12.0
#> Max follow-up: 6.0Calculating power for fixed design
Using the accrual rates and design from the previous example, suppose
we want to calculate the power if the treatment effect is smaller (\(\lambda_2 = 0.4\) instead of \(0.3\)). We use the
accrual_rate computed in the previous step.
# Store the result from the previous calculation
design_result <- sample_size_nbinom(
lambda1 = 0.5,
lambda2 = 0.3,
dispersion = 0.1,
power = 0.8,
accrual_rate = c(5, 10),
accrual_duration = c(3, 3),
trial_duration = 12,
dropout_rate = 0.05,
max_followup = 6
)
# Use the computed accrual rates to calculate power for a smaller effect size
sample_size_nbinom(
lambda1 = 0.5,
lambda2 = 0.4, # Smaller effect size
dispersion = 0.1,
power = NULL, # Request power calculation
accrual_rate = design_result$accrual_rate, # Use computed rates
accrual_duration = c(3, 3),
trial_duration = 12,
dropout_rate = 0.05,
max_followup = 6
)
#> Sample size for negative binomial outcome
#> ==========================================
#>
#> Sample size: n1 = 38, n2 = 38, total = 76
#> Expected events: 177.3 (n1: 98.5, n2: 78.8)
#> Power: 26%, Alpha: 0.025 (1-sided)
#> Rates: control = 0.5000, treatment = 0.4000 (RR = 0.8000)
#> Dispersion: 0.1000, Avg exposure (calendar): 5.18
#> Dropout rate: 0.0500
#> Accrual: 6.0, Trial duration: 12.0
#> Max follow-up: 6.0Unequal allocation
Sample size with a 2:1 allocation ratio (\(n_2 = 2 n_1\)).
sample_size_nbinom(
lambda1 = 0.5,
lambda2 = 0.3,
dispersion = 0.1,
ratio = 2,
accrual_rate = 10,
accrual_duration = 12,
trial_duration = 12
)
#> Sample size for negative binomial outcome
#> ==========================================
#>
#> Sample size: n1 = 40, n2 = 80, total = 120
#> Expected events: 264.0 (n1: 120.0, n2: 144.0)
#> Power: 95%, Alpha: 0.025 (1-sided)
#> Rates: control = 0.5000, treatment = 0.3000 (RR = 0.6000)
#> Dispersion: 0.1000, Avg exposure (calendar): 6.00
#> Accrual: 12.0, Trial duration: 12.0Accounting for event gaps
In some recurrent event trials, there may be a mandatory “gap” period after each event during which no new events can be recorded (e.g., a recovery period or administrative window). This effectively reduces the time at risk.
If an event_gap (\(g\))
is specified, the function adjusts the calculation as follows:
- Effective rates: The event rates are adjusted to \(\lambda^* = \lambda / (1 + \lambda g)\) for the sample size calculation (Zhu and Lakkis method).
- At-risk exposure: The function reports the “average at-risk exposure” \(\mathrm{E}_{\text{risk}} = \mathrm{E}_{\text{cal}} / (1 + \lambda g)\) alongside the standard calendar exposure. This provides transparency on the actual time subjects are at risk for events.
Since the gap reduction depends on the event rate (\(\lambda\)), the at-risk exposure differs between treatment groups if their rates differ, even if the calendar exposure is the same. This is a key reason why average exposure may differ between groups in the output.
Example with event gap
Calculate sample size assuming a 30-day gap after each event (approx
0.082 years). Note how the exposure_at_risk differs between
groups because the group with the higher event rate (\(\lambda_1 = 2.0\)) spends more time in the
“gap” period than the group with the lower rate (\(\lambda_2 = 1.0\)).
sample_size_nbinom(
lambda1 = 2.0,
lambda2 = 1.0,
dispersion = 0.1,
power = 0.8,
accrual_rate = 10,
accrual_duration = 12,
trial_duration = 12,
event_gap = 30 / 365.25
)
#> Sample size for negative binomial outcome
#> ==========================================
#>
#> Sample size: n1 = 9, n2 = 9, total = 18
#> Expected events: 142.7 (n1: 92.8, n2: 49.9)
#> Power: 80%, Alpha: 0.025 (1-sided)
#> Rates: control = 2.0000, treatment = 1.0000 (RR = 0.5000)
#> Dispersion: 0.1000, Avg exposure (calendar): 6.00
#> Avg exposure (at-risk): n1 = 5.15, n2 = 5.54
#> Event gap: 0.08
#> Accrual: 12.0, Trial duration: 12.0In this example, even though the calendar time is the same for both groups, the effective at-risk exposure is lower for Group 1 because they have more events and thus more “gap” time.