t-distribution Spending Function

The function sfTDist() provides perhaps the maximum flexibility among spending functions provided in the gsDesign package. This function allows fitting of three points on a cumulative spending function curve; in this case, six parameters are specified indicating an x and a y coordinate for each of 3 points. Normally this function will be passed to gsDesign() in the parameter sfu for the upper bound or sfl for the lower bound to specify a spending function family for a design. In this case, the user does not need to know the calling sequence. The calling sequence is useful, however, when the user wishes to plot a spending function as demonstrated below in examples.

The t-distribution spending function takes the form $$f(t;\alpha)=\alpha F(a+bF^{-1}(t))$$ where $F()$ is a cumulative t-distribution function with df degrees of freedom and $F^{-1}()$ is its inverse.

Usage

sfTDist(alpha, t, param)

Arguments

alpha: Real value $> 0$ and no more than 1. Normally, alpha=0.025 for one-sided Type I error specification or alpha=0.1 for Type II error specification. However, this could be set to 1 if for descriptive purposes you wish to see the proportion of spending as a function of the proportion of sample size/information.
t: A vector of points with increasing values from 0 to 1, inclusive. Values of the proportion of sample size/information for which the spending function will be computed.
param: In the three-parameter specification, the first paramater (a) may be any real value, the second (b) any positive value, and the third parameter (df=degrees of freedom) any real value 1 or greater. When gsDesign() is called with a t-distribution spending function, this is the parameterization printed. The five parameter specification is c(t1,t2,u1,u2,df) where the objective is that the resulting cumulative proportion of spending at t represented by sf(t) satisfies sf(t1)=alpha*u1, sf(t2)=alpha*u2. The t-distribution used has df degrees of freedom. In this parameterization, all the first four values must be between 0 and 1 and t1 < t2, u1 < u2. The final parameter is any real value of 1 or more. This parameterization can fit any two points satisfying these requirements. The six parameter specification attempts to fit 3 points, but does not have flexibility to fit any three points. In this case, the specification for param is c(t1,t2,t3,u1,u2,u3) where the objective is that sf(t1)=alpha*u1, sf(t2)=alpha*u2, and sf(t3)=alpha*u3. See examples to see what happens when points are specified that cannot be fit.

Value

An object of type spendfn. See spending functions for further details.

Note

The gsDesign technical manual is available at https://keaven.github.io/gsd-tech-manual/.

References

Jennison C and Turnbull BW (2000), Group Sequential Methods with Applications to Clinical Trials. Boca Raton: Chapman and Hall.

Author

Keaven Anderson keaven_anderson@merck.com

Examples

library(ggplot2)
# 3-parameter specification: a,  b,  df
sfTDist(1, 1:5 / 6, c(-1, 1.5, 4))$spend
#> [1] 0.02851967 0.08253974 0.18695048 0.38823035 0.72415039

# 5-parameter specification fits 2 points,  in this case
# the 1st 2 interims are at 25% and 50% of observations with
# cumulative error spending of 10% and 20%, respectively
# final parameter is df
sfTDist(1, 1:3 / 4, c(.25, .5, .1, .2, 4))$spend
#> [1] 0.1000000 0.2000000 0.3724396

# 6-parameter specification fits 3 points
# Interims are at 25%. 50% and 75% of observations
# with cumulative spending of 10%, 20% and 50%, respectively
# Note: not all 3 point combinations can be fit
sfTDist(1, 1:3 / 4, c(.25, .5, .75, .1, .2, .5))$spend
#> [1] 0.1000000 0.2000000 0.5000006

# Example of error message when the 3-points specified
# in the 6-parameter version cannot be fit
try(sfTDist(1, 1:3 / 4, c(.25, .5, .75, .1, .2, .3))$errmsg)
#> Error in sfTDist(1, 1:3/4, c(0.25, 0.5, 0.75, 0.1, 0.2, 0.3)) : 
#>   6-parameter specification of t-distribution spending function did not produce a solution

# sfCauchy (sfTDist with 1 df) and sfNormal (sfTDist with infinite df)
# show the limits of what sfTdist can fit
# for the third point are u3 from 0.344 to 0.6 when t3=0.75
sfNormal(1, 1:3 / 4, c(.25, .5, .1, .2))$spend[3]
#> [1] 0.3439558
sfCauchy(1, 1:3 / 4, c(.25, .5, .1, .2))$spend[3]
#> [1] 0.6

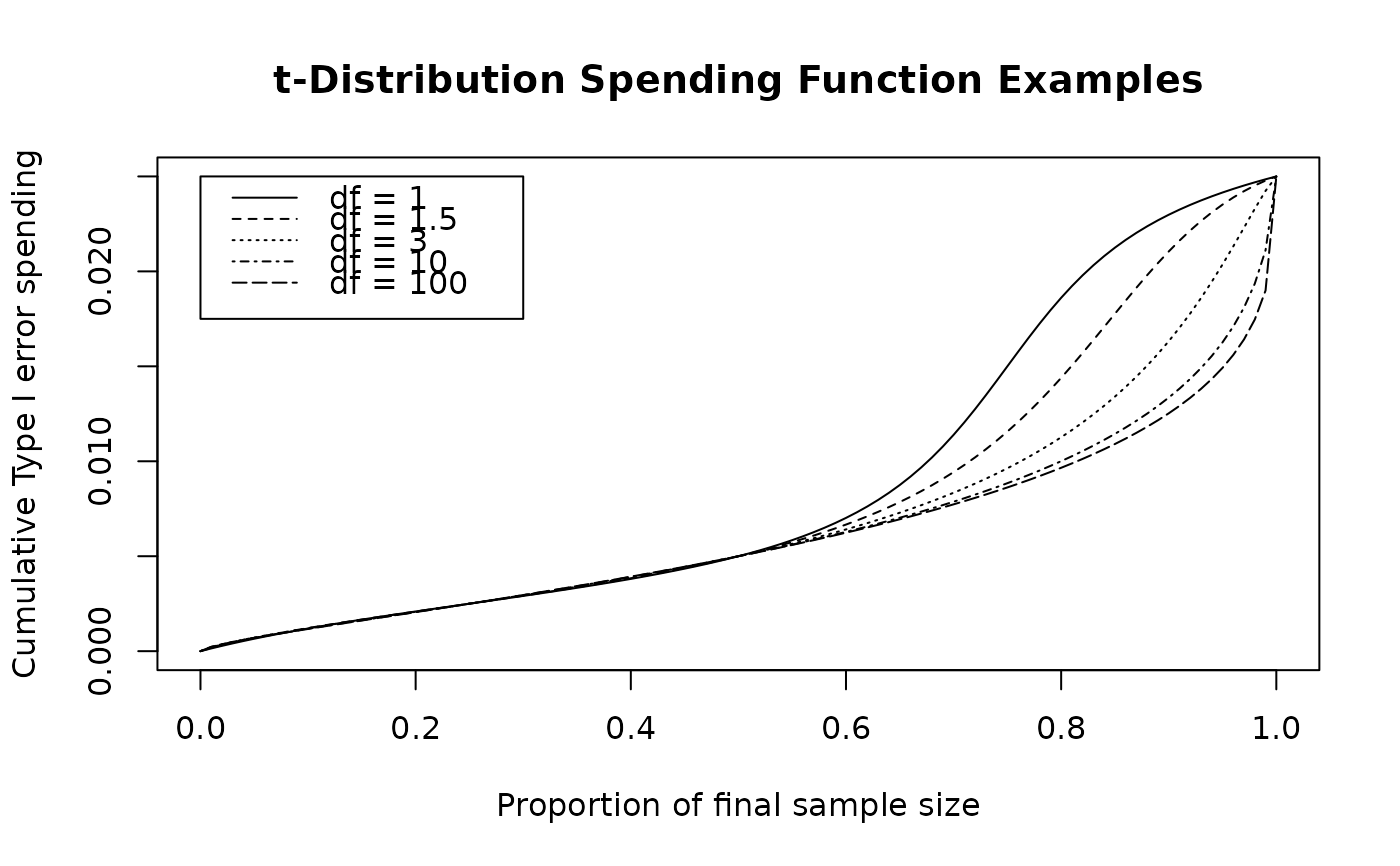
# plot a few t-distribution spending functions fitting
# t=0.25, .5 and u=0.1, 0.2
# to demonstrate the range of flexibility
t <- 0:100 / 100
plot(t, sfTDist(0.025, t, c(.25, .5, .1, .2, 1))$spend,
  xlab = "Proportion of final sample size",
  ylab = "Cumulative Type I error spending",
  main = "t-Distribution Spending Function Examples", type = "l"
)
lines(t, sfTDist(0.025, t, c(.25, .5, .1, .2, 1.5))$spend, lty = 2)
lines(t, sfTDist(0.025, t, c(.25, .5, .1, .2, 3))$spend, lty = 3)
lines(t, sfTDist(0.025, t, c(.25, .5, .1, .2, 10))$spend, lty = 4)
lines(t, sfTDist(0.025, t, c(.25, .5, .1, .2, 100))$spend, lty = 5)
legend(
  x = c(.0, .3), y = .025 * c(.7, 1), lty = 1:5,
  legend = c("df = 1", "df = 1.5", "df = 3", "df = 10", "df = 100")
)