7 Two-sided and other design types
We have worked exclusively with 2-sided, asymmetric designs with non-binding futility bounds so far. Now we move on to symmetric 2-sided designs, asymmetric designs with binding futility bounds and 1-sided designs. We also provide more background on binding versus non-binding futility bounds.
7.1 Overview
In this chapter, we briefly talk about 2-sided designs, superiority-only designs, and asymmetric designs with binding futility bounds. These design types are selected from the “Boundaries” tab (Figure 7.1). For any of the designs discussed previously, try switching between 1) asymmetric, non-binding, asymmetric binding, 3) symmetric, and 4) superiority-only to see how sample size and bounds change.

Perhaps the most common designs are the asymmetric designs with non-binding futility bounds we have discussed so far. These designs control Type I error even if a trial continues after a futility bound has been crossed, making them most acceptable as pivotal trials intended to be key for regulatory approval.
7.2 Two-sided symmetric designs
Two-sided symmetric designs are useful for comparisons where it is not clear which treatment might be better than the other. This may be the situation when two approved treatments are compared to each other. The bounds are symmetric about the null hypothesis (normally no treatment difference), as seen in Figure 7.2.
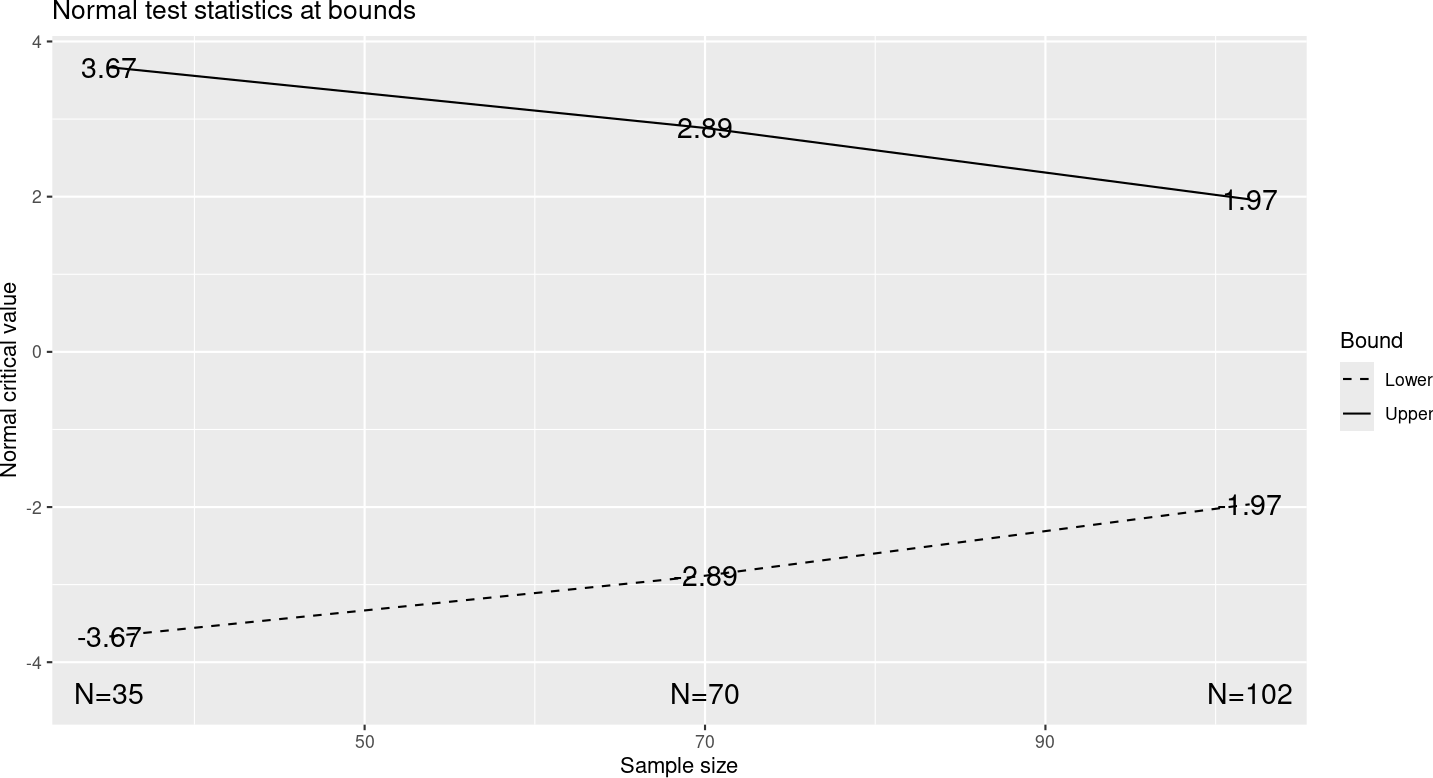
Other than selecting “Symmetric” on the “Boundaries” tab, this design is identical to that in Chapter 2. Only the upper spending function is specified for symmetric designs as the same spending function is used for the lower efficacy bound. You will see that you are not given the option to select a lower spending function when a 2-sided design is selected.
7.3 Superiority-only designs
Superiority-only designs are also referred to as one-sided designs or efficacy-only designs. These designs might be used when a new drug is understood well enough to have no need to stop for futility. This may also be appropriate for a trial that enrolls quickly where efficacy may only be shown late. That is, all patients may be enrolled before any interim analysis can be performed.
7.4 Binding futility bounds
For Phase 2 or other trials not intended for regulatory approval, an asymmetric design with a binding futility bound may be useful. Sample size requirements are smaller than non-binding designs and the bounds are tighter, making it easier to stop early. In these cases, the sponsor may be willing to make a strict assumption that the trial would stop early if a futility bound were crossed. Designing with binding futility bounds is specified under the “Boundaries” tab. Try switching between non-binding and binding designs to see how the sample size and bounds change. Generally, these designs are not considered acceptable for regulatory approval as Type I error increases above that specified if futility stopping rules are not obeyed, which may be an option a sponsor or data monitoring committee wants to consider as a trial is executed. However, there can be some savings in sample size and such a design might be considered for a non-pivotal Phase 2 study.
7.5 H0 spending
We reconsider the Kim-Tsiatis design (vary enrollment duration) design of Section 5.2. In the “Boundaries” tab, we change the “Testing” input to “Asymmetric, non-binding [H0 spending]”; see Figure 7.3; you can load the design from kim-tsiatis-h0-spending.rds.
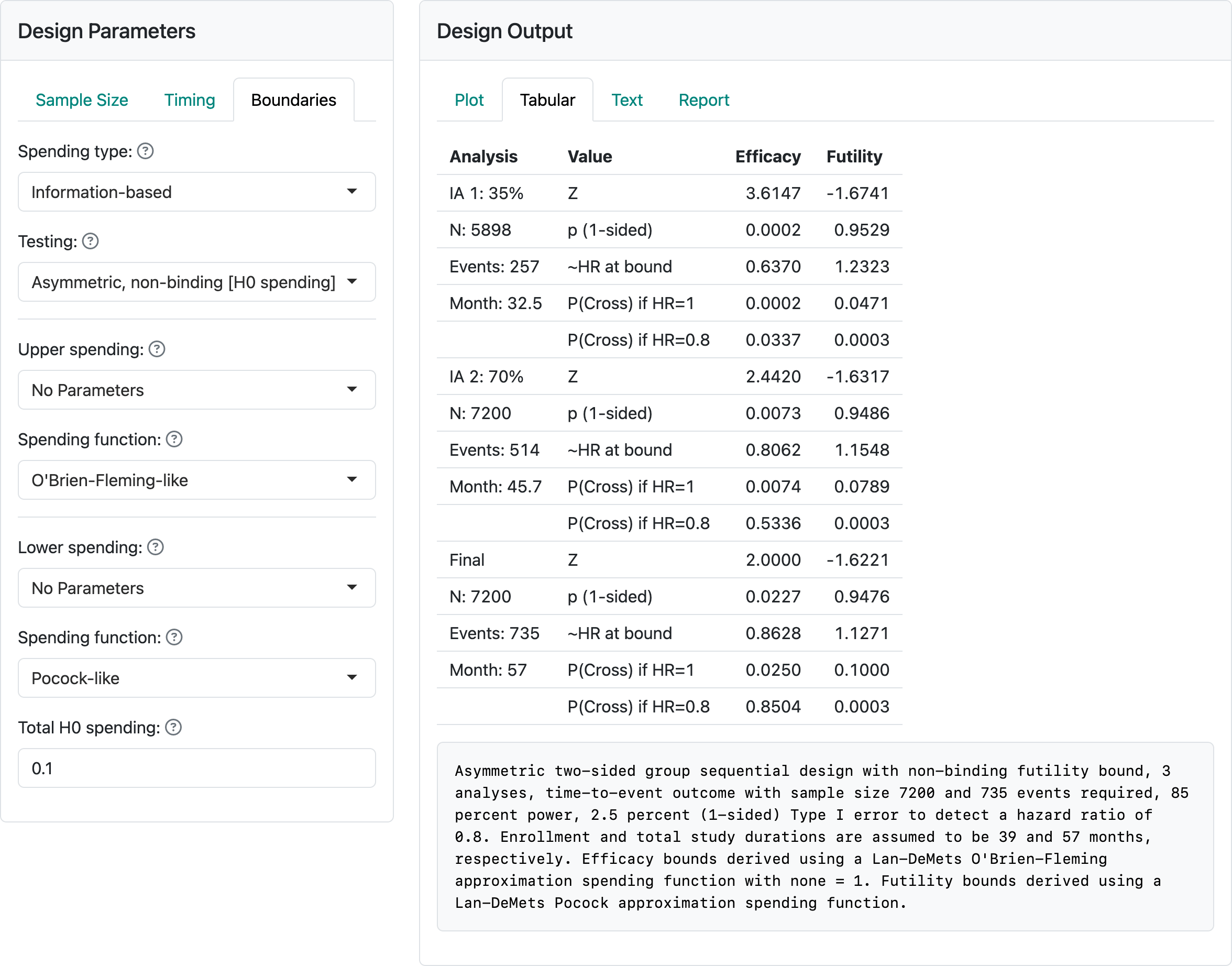
We have set “Total H0 spending” to 0.1 and changed the lower spending bound to “Pocock-like”, meaning the Lan-DeMets spending function (Lan and DeMets 1983) approximating a Pocock bound (Pocock 1977). There is no indication in the caption that spending is under H0 and the “with none = 1” in the caption is superfluous. In the next-to-last line in the table in the “Futility” column we see the cumulative probability of crossing the futility bound under the null hypothesis is 0.1 as specified in “Total H0 spending”. A Pocock bound (Pocock 1977) has equal \(Z\)-values; again, in the futility column the \(Z\)-values are approximately equal (\(-1.67\), \(-1.63\), \(-1.62\)), each having a nominal 1-sided \(p\)-value in favor of control near 0.05 (\(= 1 - 0.95\) as seen for each analysis). Thus, the bound would not recommend stopping for futility unless there were a nominal \(p\)-value of 0.05, 1-sided in favor of control. This bound is compatible where there is desire to get to the end of the trial unless there is an ethical issue with continuing. It may be useful where there is a possible delayed benefit over time or potential for the patient population to change with time; e.g., with COVID-19 the prominent virus strain changed with time.